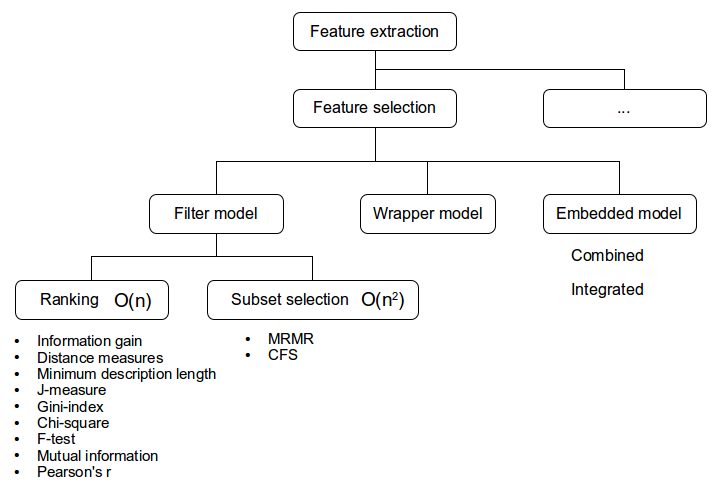
Feature selection
3 okt. 2013We repeated the lecture from Machine Learning 1, but now with deeper discussions on what feature selection is. We know from the machine learning model that we always have to start by measuring properties of something we want to classify or predict based on. We want the machine to generalize and in supervised learning we give it examples of known classification. Figuring out what properties to measure is probably the most important step, but also limited to what is practical to measure. In between this first step and feeding a learning algorithm whatever it is designed to handle we often do preprocessing of the properties we have.
This can be noise reduction in general, filling of missing data, normalization and different other techniques. Then the question is: Do we actually need all of the features for the specific task at hand? We know we pay a price for each additional feature as many of the learning algorithms have complexities much higher than linearly with the number of features. We also know based on the "no free lunch" theorem that adding more and more features won't help in the task of classifying since all classification is based on a bias of preference. If we want to separate blue items from green items, then coming up with a thousand measurements not correlated with the color will only contribute to making the object look different in other ways. Ideally we would start off with only the relevant features for the task. Then again, if we want a learning machine that does not rely on humans initiating it, then something else is required. Something similar to what makes humans tell what is important.
One solution could be to come up with a lot of measurements, preferable not biased, and then let an algorithm decide on whether or not any of them are useful, either alone or combined. This is called feature selection. There is another term feature extraction where the goal is to create new features based on existing ones. The goal can be the same, to limit the amount of features such as what principle component analysis (PCA) does by transforming the data into another space where most of the information can be expressed using fewer dimensions.
Based on lecture material
First we look at feature selection, where we want to remove redundant and irrelevant features. Degree of redundancy is a measure of whether given we know one of set of variables, then we also know what the other will be. Lets say we measure age in seconds after birth, years and seasons. They have different level of precision but they all tell the same story and we only need one of them. Preferable the one with the best accuracy.
Irrelevant features are things we measure that is actually not important for the task at hand. Lets say we want to classify an object as either a car or house. Interesting things to measure might be volume, price, color, main building material and average speed. We know that houses have larger volume and usually higher price tags than cars, that color is not relevant at all, and that houses are usually not moving and built using different materials. In reality we would still find some correlation between most of these attributes. We have very expensive cars, we might observe a house being moved and in some areas houses tend to confirm to particular color choices. What we want are attributes that cause the classification and try to remove attributes that are just correlated with the classification labels used.
We were presented some current methods. filter methods and wrappers. There is also a third category called embedded and according to teaching this is when filter and wrapper methods are applied together, like first filter then wrapper. Another definition (according to Wikipedia) is that embedded is used for learning algorithms that has this feature selection process as part of the algorithms. This makes sense as embedded means "integrated". Perhaps a better word for the first definition is "composite". Anyway..
Filter models perform ranking of features without any dependency on the classifier while a wrapper methodology is using the performance of a machine learning algorithm as the criteria for what subsets of features to keep. Filter methods come in two flavors: independent ranking (ranking) and subset ranking (subset selection). The first is the fastest one in terms or speed as each feature is assumed independent. The next logical step is to look at combinations of features and we know the number of combinations grow exponentially. Taking it even one step further we can use the machine learning algorithm itself and cross validation as the criteria. This is what wrappers are and they tend to take even more time as the training of the model must be performed for all combinations of attributes.