First we discussed our background, and what we wanted to learn during this course. The main conclusions were:

• Support Vector Machines, a supervised popular learning algorithm
  
• Heuristic search methods
  
• Genetic algorithms
  
• Neuro fuzzy approaches (because their rules are human understandable, good in court)
  
• Bayes neural network (causality)
  
• Gaussian mixture models (unsupervised)
  
• Random forest
  

We then continued on the SVM lecture, but were distracted and lead off track all the time explaining other stuff like:

• PCA versus LDA: In principle component analysis we look at the data without caring for any class labels. We just want to know how much variance there is in each attribute (dimension). It is calculated by finding eigenvalues and eigenvectors and we get generalization. Linear disciminant analysis seems to be a term describing methods for finding linear functions of attributes separating one class from another class, hence we get separability. As far as I understand, SVM is a subset method of LDA.
  
• Ugly duckling theorem: More features is not necessary better. The Theory actually says that given we measure enough properties of lets say item A, B and C, the more different each items will be. Classification works because we are selective in what we measure and classification is always biased.
  
• Curse of multidimensional: Workload often grows exponentially with more features
  
• Reduce empirical risk: Use cross validation to see how stable the algorithm is at different cross sections of the test data. Emperical risk is that a classifier can work good on test data but does not have to work good on unseen data.
  
• No free lunch theorem says that any algorithm, if above average (good) at a a subset of problems, then is must be worse than average at other subsets. There are cases where this is not true, but the reason for the theorem is that in general when we want to get better at a particular task, there will be tasks that can't be handled. One algorighm might be best for a particular situation, but there are equally situations where this algorithm will perform very bad.
  
• Term cononical: True form, original
  

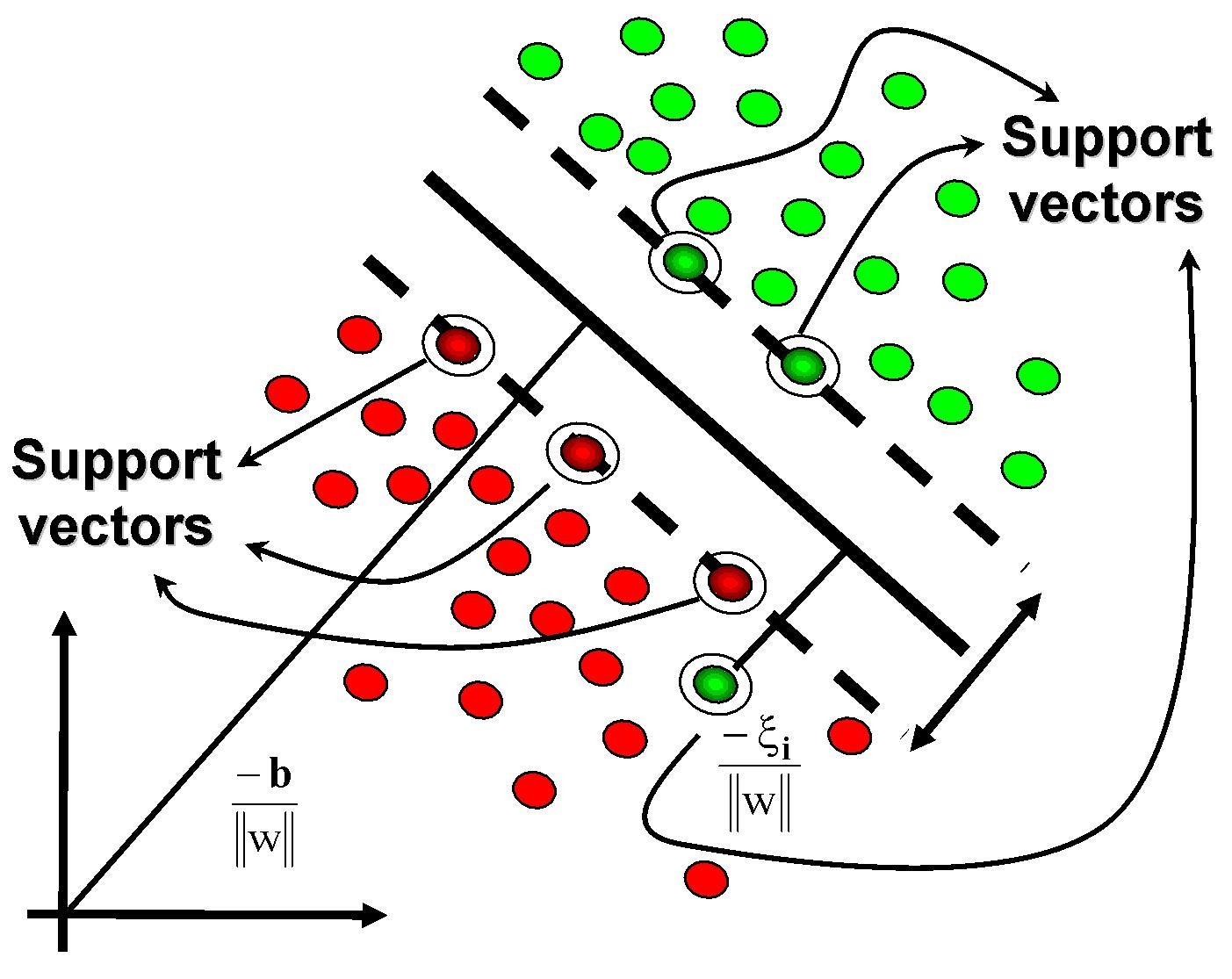
We began going though some slides of SVM. It builds on linear discriminant functions. Goal is to maximize a function representing the total margin between a hyperplane and the evidence available (test data) For speed we turn it into a minimization problem and use quadratic programing and Lagrange multipliers to solve. Quadratic programing are optimization methods for finding solutions given linear constrains. The SVM will try to find the linear separator with best margin between two classes. Only some of the samples will limit the amount of margin that can be achieved, and they are called support vectors. When the data is not linearly separable we can introduce slack so that classes on the wrong side of the margin can be ignored to some degree.

The first assignment is to program our own SVM in any language we want, without using any libraries except for solving the optimization problem.

http://www.cac.science.ru.nl/people/ustun/SVM.JPG