Clustering is an unsupervised meaning we don't know the correct classification or value. In other words, we are trying to group "similar" things. Similar could be measured with many different distance / similarity measures.

We separate between hierarchical and partitional methods. Hierarchical vs partitional clustering.

Hierarchical
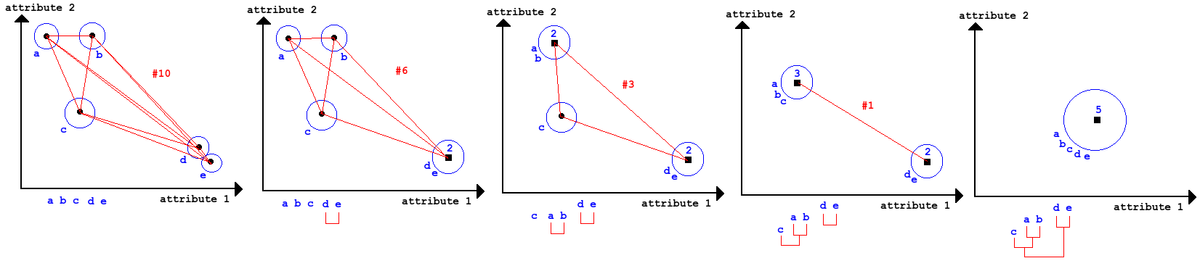
"Try all combinations of everything" - very computational expensive, but we can afterwards build a tree and decide then how many clusters we would like.
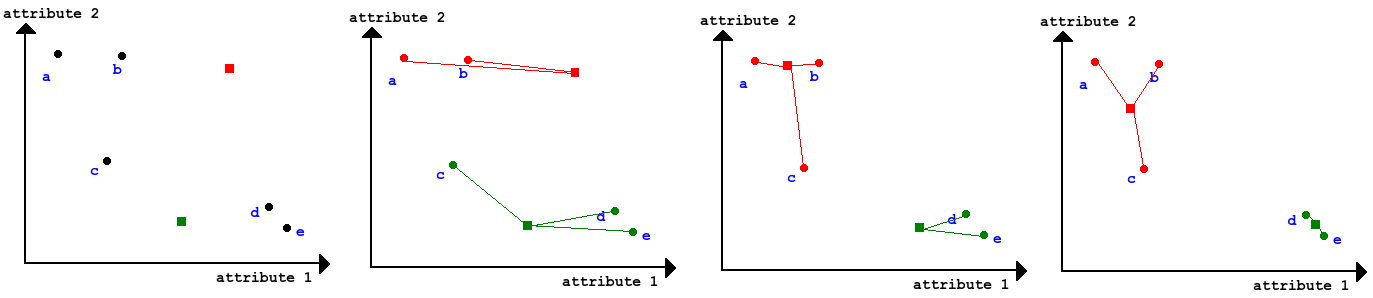
Can be bottom up: Group two most similar things until all things are grouped (Agglomerative). It can also be top down: group everything and split up most dissimilar things until all things are in individual clusters (divisive).

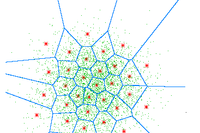
Partitional
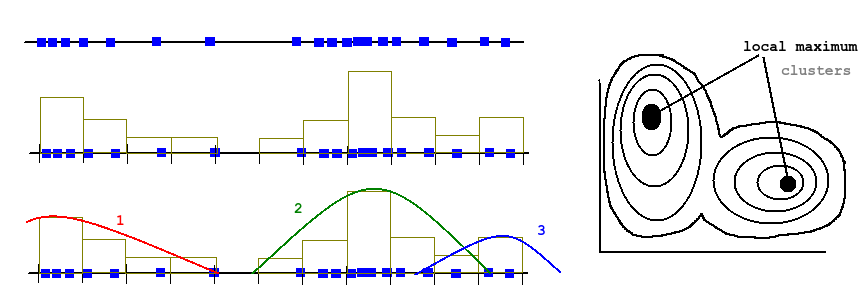
Since we got limited computational resources, we can make some trade off's: We decide on number of cluster (k) and we only calculate the distance for every sample to the current cluster centroid (center), then have the centroid grab (sample choose) the closest distances. Then we move the centroid to the average position of whatever the centroid grabbed. This is called k-means.

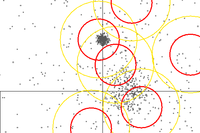
K-means by Andrew Hg (Stanford)

• 14-1
  
• 14-2
  
• 14-3
  
• 14-4
  
• 14-5
  

A variation on k-means is the c-means. It's a fuzzy algorithm meaning cluster boundaries are not binary, but instead each sample belongs to each centroid with a percentage (probability).

Tree more methods were mentioned during lecture:

Gaussian mixture model: This is actually a density estimation algorithm.
www2.it.lut.fi/project/gmmbayes/

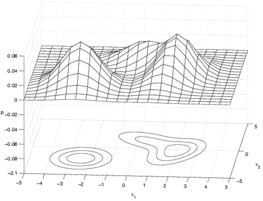
Vector quantization: ???
data-compression.com/vq

Canopy clustering: ???
cwiki.apache.org/MAHOUT/canopy-clustering

Hierartical clustering (Agglomerative)

import sys
import math
import itertools


def minkowski(a, b, degree, weights):
	degree = float(degree)
	if degree < 1:
		print('Minkowski: Not defined for lambda less than 1')
		sys.exit(1)
	result = 0.0
	dimensions = len(a)
	if dimensions != len(b):
		print('Minkowski: Samples are not of same dimensionality')
		sys.exit(1)

	for d in range(dimensions):
		result += math.pow(float(weights[d]), degree) * math.pow(math.fabs(float(a[d]) - float(b[d])), degree)

	return math.pow(result, (1 / degree))

def eucledian(a, b):
	return minkowski(a, b, 2, [1] * len(a))

def cityblock(a, b):
	return minkowski(a, b, 1, [1] * len(a))

def merge(a, b):
	dimensions = len(a)
	if dimensions == len(b):
		result = []
		for d in range(dimensions):
			result.append(float(a[d]) - ((float(a[d]) - float(b[d])) / 2))
		return result
	else:
		print('Merge: Samples are not of same dimensionality')
		sys.exit(1)

def print_samples(samples):
	string = ''
	for s in samples:
		string += '%s=%s ' % (s['id'], s['data'])
	return string

samples = [
		{'id': 'a', 'data': [3, 4]},
		{'id': 'b', 'data': [4, 5]},
		{'id': 'c', 'data': [9, 6]},
		{'id': 'd', 'data': [10, 3]},
		{'id': 'e', 'data': [11, 1]},
		{'id': 'f', 'data': [4, 2]},
]
print('Starting clusters: %s') % print_samples(samples)

while len(samples) > 1:
	# 1 calculate all current combinations of distances
	combinations = itertools.combinations(range(len(samples)), 2)  # get combinations of two from sample range (want indexes)
	similarities = []
	for c in combinations:
		a = samples[c[0]]['data']
		b = samples[c[1]]['data']
		similarities.append([eucledian(a, b), c])

	most_similar = sorted(similarities)[0][1]  # the two most similar samples
	id_first = samples[most_similar[0]]['id']
	id_second = samples[most_similar[1]]['id']
	print('Most similar: %s and %s') % (id_first, id_second)

	# 2 merge the two with smallest distance
	new_cluster = merge(samples[most_similar[0]]['data'], samples[most_similar[1]]['data'])
	samples.append({'id': id_first + id_second, 'data': new_cluster})
	indices = most_similar[0], most_similar[1]
	samples = [i for j, i in enumerate(samples) if j not in indices]
	print('New clusters: %s') % print_samples(samples)