So, what does searching have to do with machine learning? I guess the best answer is that a machine learns by searching for the best rule in a given hypothesis space. Brute force knowledge by searching all possible∕probable solutions.

A good source at "learn artificial neural networks"
Graphs at msdn

No matter what search method is being used, it is important to remember that the total time to get an answer includes setup time and time to analyze the answer the algorithm got in order to verify it is correct. Using a lot of time optimizing the algorithm at the cost of complexity is not always a good idea, unless the same type of problem is being repeatedly solved.

Lets say you want to find the best solution to a problem using a computer. An algorithm to find any solution requires time and space. Time is simply the number of operations necessary to complete and will depend of the speed of the processors involved. A task that can be broken down into multiple independent tasks can be parallelized so that multiple processors can work on it simultaneously, giving that algorithm a small edge. Space is the maximum amount of memory required to keep track of temporary calculations and state of the algorithm. If an algorithm keeps consuming more and more memory while running, it will either have to stop or first start slowing down because of disk paging and then stop when no more space is left. What we want is to solve any problem as fast as possible within the spacial limits we got.

We can think of to kinds of solution domains. Problems with an infinite or unknown solution domain, and problems with a finite known solution space. An example of the first might be trying to write out one third (1/3) in decimal form. No matter how far we go, we can always find an infinite number of new decimals. A cryptographic algorithm using a 56-bit key has 2 power of 56 possible keys, and if all possibilities are tried, we are certain that the (only) solution is found.

This is important to realize because when the best solution is to be found, best must be defined. It could be the optimal solution, a solution that can not be exceeded by another solution, like finding the cryptographic key (There might be problems with several optimal solutions). If the optimal solution is infinite, then time complexity is infinite and you will never finish. A compromise solution is a trade of, either in time, space or precision.

A way to visualize the search space is to think of it as a tree. It could be a binary tree with only two children per node, or there might be a variable number of children nodes expanded from a node. The difference between the search algorithms are basically what order to we travel (search) the tree, and when do we know we got a good (enough) solution.

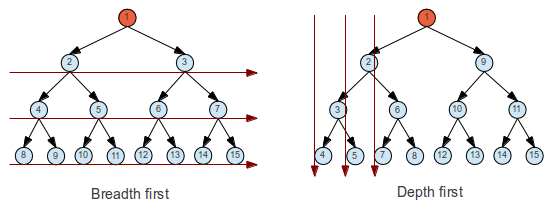
(In order to understand these graphs, it's important to distinguish between checking the node and adding to the queue)

The most naive methods are called exhaustive search: They can be breadth first or depth first. Breadth first require that the algorithm must remember all the children not yet visited while searching the current depth. This queue gives an exponential space complexity growth. Depth first will travel all the way down one path before exploring any more at the same depth. This search will not work if the depth is unlimited. A compromise is a limited depth search, and can be followed by increasing the depth limit by one if no match was found (Iterative deepening).

The above mentioned might be the only way to solve a problem where there is no pattern in the search space (tree). If however the tree has a pattern, like a sorted tree, searching for a match can be reduced to a look up. Certain paths can be excluded because they cannot contain the answer we are searching for.

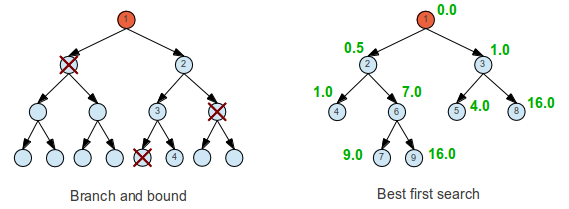
Bounded exhaustive serach (Branch and bound) is a method that can be used if the problem can be divided (or branched) in smaller subsets and "conquered" (fathomed) by estimating the solution and then excluding impossible solutions. It's still exhaustive because all the "not ruled out" events must still be brute forced.
Video: Backtrack / Branch and Bound

In best-first search the idea is to start with the most likely paths before the less likely paths. It's based on "breadth first" but instead of always following the same search pattern, it is determined by some criteria.
Branch and Bound Algorithms

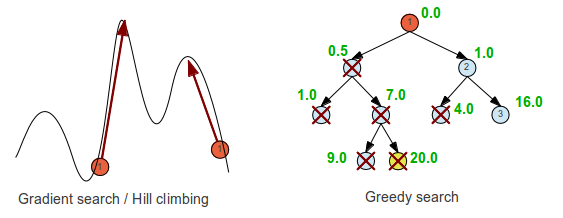
A Greedy search always chooses the local best path, and hopes it will lead to the global best path. Some kinds of problems like finding the minimum money units for a sum of money, always give the optimal solution. If we extend the search to include searching in the n-th best paths for each local problem we call it beam search, and I guess if we include them all we end up back to an exhaustive best first search. (Not sure of this one).

Hill climbing and Gradient search require knowledge of the value of moving in different directions and they both always moves in the direction that leads to greater or lesser values. They will always find the local maximum or minimum, but whether they hit the global max or min depends on the initial starting point, and are thus random.
Qualitative vs Quantitative (has some thoughts on hill climbing about 25 min in)

A totally random selection of combinations in the hope they will give the optimal solution is another very easy but very nondeterministic method. It's often called Monte Carlo. A very complex method utilizing random selection (inspired by evolution and DNA) is Genetic algorithms (GA). The main problems in genetic algorithms are to define what "fit" is (who shall survive) and not being too biased, then define how "genes" are transferred to children (called crossover) including some randomness (mutation). The most fit are kept for each run, initiating the mix of genes to create the next generation. Another problem is that the initial gene configurations might hinder some possible (optimal) outcomes. GA is extremely slow...

"Some weak solutions might have good parts"

This video Neural Network Demo illustrates the evolution of a car trying to navigate without crashing. At the end of the lecture, we saw a video of GA used to learn how to play Mario. Video: Mario AI - a comparison (It's not the same video, but it illustrates how searching is used to always determine the optimal out of a varying pool of possible outcomes is selected.

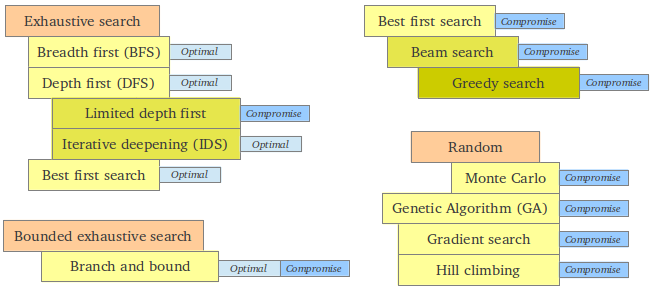
This video lecture CS3 lecture 42: Heuristics - Simulated Annealing gives a good overall understanding of the different search approaches. At around 25:00 he starts to group the different algorithms. The basic steps are "Do we have to solve the problem?", "Brute force", "Can the problem be simplified" and "is there a pattern to the solution space". The last being heuristic meaning we have some criteria to determine if a given combination is more or less correct.

All CS3 lectures I found related to search algorithms:

• CS3 lecture 33: The Greedy Method
  
• CS3 lecture 34: More Greedy Method
  
• CS3 lecture 35: Divide and Conquer
  
• CS3 lecture 36: The Phileas Fogg Problem
  
• CS3 lecture 37: Backtrack Branch and Bound
  
• CS3 lecture 39: Qualitative vs Quantative
  
• CS3 lecture 41: Dynamic Programming vs Memoisation
  
• CS3 lecture 42: Heuristics - Simulated Annealing
  
• CS3 lecture 43: Simulated Annealing (part2)
  

From exercise

• Stopping criteria: Limit number of itterations, define convergence.
  
• Convert "minimazation problem to maximization" trick: invert the problem, like finding 1 - the probabilty of the oposite case.
  
• Example of generic algorithm
  
• Example of gradient descent: Problem with local minimum depending on starting position, step size and number of iterations.