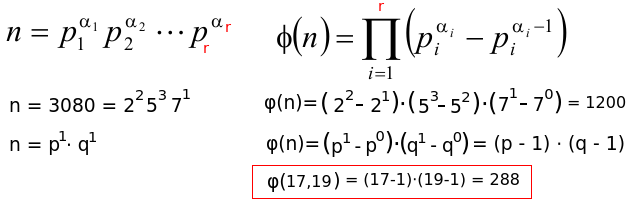Cryptology1 (part4)
23 sept. 201221. September 2012: Lecture #4: Asymmetric ciphers
Reading this week
- Trappe chapter 3,6 and 7
- Menezes chapter 1,2,3,4 and 8
There are many situations where a pre shared key scheme is very difficult to implement due to a large number of participants. Like online banking. With a symmetric cipher with n number of participants every participant would need to be given a unique random key for every other participant. An asymmetric cipher uses different keys for encipherment and deciphermen, and is often refereed to as a "secret and public key scheme". Each node generates this pair of keys, keeping the private key secret and offers the public key for everyone, published in a "phone book". Encipherment of a public key can only be read by the node who got the corresponding secret key. The other way around everyone could verify node X is the source of a signed document since one node X knows the secret key that would let the corresponding public key decipher it.
An analogy mentioned in the book goes like this Lets say Alice wants to share secrets with Bob and Charlie. They all make a box with a padlock only they themselves has the key for, and offers these unlocked boxes to anyone wanting to send them a secret message (these boxes are digital and can be copied with ease). Both Bob and Charlie can make copies of Alice box, put messages inside it, lock it and send it back to Alice. She is the only one able to open the boxes.
Because of this a scheme where keys could be generated and exchanged on an insecure medium is what we want. Something still has to be shared in advanced to achieve identification, but was not the focus of this lecture (like in every browser there is a list of trusted 3rd parties signing on behalf of businesses and organizations.)
Diffie and Hellman defined asymmetric ciphers in 1976. Their consideration was primary key exchange. They postulated 4 conditions but did not suggest any implementations at the time. Let K be the finite key space, M be the finite message space. We then have two transformations: E (encipher) and D (decipher).
- Encipherment is the inverse of Decipherment for every Key
- For every Message and Key, Encipherment and Decipherment is easy to compute
- For almost every Key, it is computational infeasible to derive D from E
We can make E public since it won't compromise D
- For every Key it is feasible to compute inverse pairs E and D from the Key.
So we got a definition of such a system, but can it be realized and what would the security of it be? We still can't prove such a system is theoretically possible to construct, but there are functions, so called trap-door one-way functions that are believed to be candidates.

RSA (Rivest-Shamir-Adleman) proposed similar properties as Diffie Hellman in 1977:
- D(E(M)) = M
- Both E and D are feasible to compute
- Publicly revealing E does not reveal a feasible way to compute D
- E(D(M)) = M
The first tree are the same as Diffie Hellman, and the criteria's of a trap-door one way function. The 4th is new and says this function must be a permutation, a one to one mapping, and is used in digital signing. Trap door means it is revertible if you know the key.
RSA procedure
RSA uses prime number problems, and to be secure it requires relatively huge numbers (keys) to be secure. We used to have 1024bit keys, but are now moving to 2048bit because attacks on 1024bit are getting closer to succeeding. Compared with 128bit keys for symmetric ciphers, it is important to remember the security of these asymmetric ciphers are assumed safe because we don't know of any method of solving the "one way function" the other way around. We haven't proved such a method does not exist. Also the speed of encipherment and decipherment is much slower than symmetric ciphers. One usually uses asymmetric ciphers to authenticate and exchange keys for a much faster symmetric cipher.
RSA utilizes the fact is it very hard to factorize the product of two very large primes. Other potential problems are elliptic curve problems.
Generate the keys
- Find two large distinct random primes p and q. They should be of about the same size (in bits)
- Compute n = p ⋅ q
- Compute Euler's function: φ(n) = (p-1)(q-1)
- Find a random integer e such that gcd(e,φ(n)) = 1. Remember 1 < e < φ(n).
- Compute d such that gcd(e,d) ≡ 1 mod φ(n)
The public key is (n,e) and the private "trap door" key is d
Use the keys It is important to remember that when a message is to be enciphered, one has to use the other party's public key for n and e. When decipherment is done, one has to use the the own secret key. Also the message m has to be encoded in the message space (1 to n since the number is mod n).
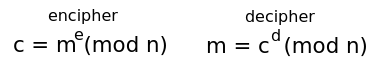
There are several problems...
- How to find two huge prime numbers
This procedure require a guess and continuous testing. Chose a huge number m and add one if it is even. (primes are not even). Test m, and if not prime test m + 2 etc. The probability of m being a prime is 1/ln(m). The function for testing prime is often a probabilistic algorithms like Solovay-Strassen or Miller-Rabin. They are fast, but have a small probability of reporting faulty. Algorithms like Las Vegas always give a correct answer, but they could take a very long time to complete.
Number of tries with a 512bit number would be ≈ 177 (when the 512bit number is used to represent positive and negative numbers) and about 710 tries for a 2048bit number.Lets chose 17 and 19 with n=323
- Calculate φ(n) in general

- Calculate gcd (greatest common divisor) for two numbers (Euclidean algorithm) for finding a suitable e

Public key (n,e) = (323, 5)
- Find multiplicative inverse d by means of extended Euclidean algorithm.
A multiplicative inverse is only possible if gcd(m,e) = 1

- How to do modular exponentiation
The last difficult part it the exponentiation with modulo. Lets say Alice made the public(n,e)=(323,5) and private(d)=(173). Bob wants to send the message "8" to Alice. This is what happens