Cryptology1 (part2)
2 sept. 201231. august 2012: Lecture #2: Symmetric ciphers (1/2): Stream ciphers
Reading this week
- Menezes ch5,6
Problem with Vernam cipher (one time pad) is time to generate key material (physical processes as source are slow), and the problem of distribution of key material. We can sacrifice the perfect security by replacing a random key with a keyed deterministic algorithm. Output sequence is a pseudo-random key used in the same way as in Vernam cipher and is called the "running key". We still need to seed the initial state of the finite state machine and that key must still be distributed. Can be very small (128bit). Also, Internet cannot be used in space!
Running key (pseudo-random noise (PN) sequence) must follow these criteria's:
- Long period: It will be ultimately periodic and it might have an a-periodic start! Extremely long periods are not difficult to design.
- Pseudo randomness properties: Golombs postulates
- Unpredictable: Linear complexity. Given a part of the sequence of any length the cryptanalyst cannot predict the next digit
Golomb's postulates
- Difference of 1 and 0 not overcome unity (must be not be more than one in difference) within a period
- A run is defined as one or more 0s or 1s in a row (0s = gap and 1s = block). The probability of either 0 or 1 after a run has to be 50%. Same amount of blocks and gaps. Statistically a 3-run has twice the count as a 4-run.
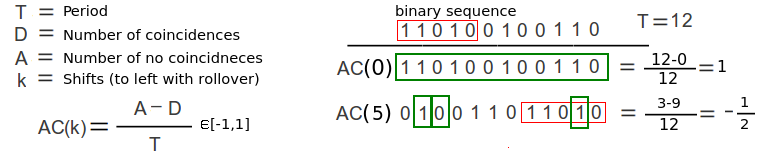
- Auto correlation out of phase must be constant for every shift possible (Auto-correlation is when you shift and compare number of coincidences (number between -1 and 1)
Auto correlation
How to build the PN sequence generator
Linear congruencies
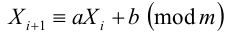
- a,b,m and the initial value of X can be used as the key
- Not secure since it is possible to deduce the parameters if you have a long part of the output sequence.
Feedback shift registers
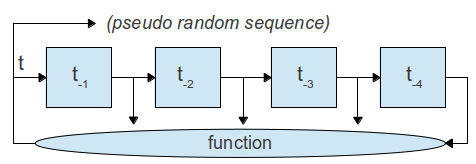
A number of flip-flops connected in series. For every clock pulse the value of each flip-flop is pushed to the next one. A feedback function takes the states between these flip-flops every clock pulse and returns a value feed to the start of the series at the same time every flip-flop shifts. The key would be the initial state of the shift-registers. The function must NOT be singular and we avoid singularity by making sure the last position of the feedback function is an XOR operation. If the function is singular, it will have sub-cycles. Writing the function in algebraic normal form is a part of cryptology2. (Using only XOR and AND logic). A DeBruijn graph is used to visualize cycles.
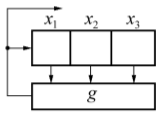
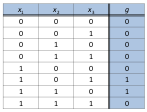
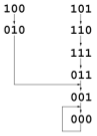
- Linear feedback shift registers (LFSR): When only XOR is used (in algebraic normal form) to express the feedback function (g).
- None-linear feedback shift registers: When AND operations is also included.
Linear FSR
The initial state cannot be all zero, thus largest number of states is
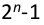
Every feedback function can be expressed as a feedback polynomial:
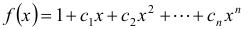

- Reducible: can reduced to something with a product (remember XOR logic) → many (different sizes) cyles
- Irreducible: "prime" polynomial. Can have several cycles but they are of equal length
- Primitive: special class of irreducible: Only one cycle (except all zeros) (Part of cryptology2) ← The one we want!
Linear complexity:
We want high linear complexity which means it will be very hard to predict the next bit in a bit-stream. The Berlekamp-Massy algorith says any bit-stream can be written as a polynomial and it's initial state (+ a delay line). The polynomial might be very long though and the computational complexity is quadratic. A single linear feedback shift register has low linear complexity (?) and ways to increase it is:
- None-linear filter: Different functions generating running key from the loop back logic. In general difficult to calculate linear complexity
- None-linear combiner: Output of several LFSR's input to a function generating the running key. Must use confusion and diffusion principles when designing. Important to consider statistics (balanced: equal number of 1s and 0s) and correlation (avoid running key to be correlated with one or more of the LFSR's). Correlation attack: "Divide and conquer": We want high none linear order and correlation immunity at the same time and they are opposite. A trade off. (See Geffe's generator page 65 for example of balances but correlated output)
- Decimation: Only use parts of the output from a LFSR. One can use a LFSR's output to decimate another called a binary rate multiplier BRM or use a LFSR to clock another LFSR called shrinking generator. You use output of 2. LFSR when 1. LFSR is 1 as running key.
None-linear FSR
A systematic method for analyzing them does not exist, mathematical theory not well developed. Sequences does not satisfy Golomb's 3. postulate. (0⋅0=0, 0⋅1=0, 1⋅0=0 and 1⋅1=1 → one 1 and tree 0 when multiplying)