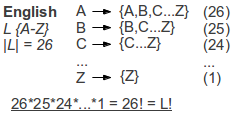24. august 2012: Lecture #1: Classical cryptography

Reading this week

• Trappe ch1,2,15
  
• Menezes ch1,2
  
• Communication Theory of Secrecy Systems by C. E. Shannon
  

---

Concepts

Crypto from Cryptos (Greek): Secret

"-logy" from Logos (Greek): Language/meaning/science

Cryptography Designing crypto algorithms

Cryptanalysis Science of breaking crypto algoritms

Cryptology Both of the two above (collection term)

Involution When encipher and decipher method are the same

Kerckhoffs's principle A cryptosystem should be secure even if everything about the system, except the key, is public knowledge

Information or message to be shared securely is called the plaintext. After being transformed by a crypto function locally, using a key only you and the intended receivers of the message know. The output is called the cipher-text and the process enciphering. When our intended receivers do the inverse crypto function deciphering, they will get the plaintext. When someone not intended for the message tries to break our cipher-text without knowing the key using cryptanalysis, we call the process decryption. American literature use decrypt for both decipher and decryption.

Cryptogram Cipher text when we don't know the key

Types of crypto algorithms

• Symmetric: Stream ciphers and block ciphers, same key for encipher and decipher. Pre shared key delivered to all parties in advance via a secure channel.
  
• Asymmetric: Different key for encipher and decipher. Private/public key pair. Each party has own private and public key. Depends on a problem easily solved in one direction but very hard the other way around. It works like this: Alice sends a box with a padlock only she has the key for to Bob. Bob receives the box, but his secret message in the box, locks the padlock and sends it back. If Alice wants to send a secret to Bob, he would have to supply the box. The public key is the box and the private key opens the padlock. The main problem with this system is trust. How can we know who is the origin of the box we are currently using? (This can be solved by trusting a 3. party signing the public keys)
  

Stream ciphers

• Transformation applied to every symbol/bit/character
  
• Very fast (compared block ciphers and even more so when compared with public key crypto)
  
• Military use (they are considered very secure when implemented correctly)
  
• Examples: RC4
  
• USA has export restrictions on stream ciphers and are often classified (Against Kerckhoffs's principle)
  

Block ciphers

• Apply transformation on a block at a time (128bit a time like in AES)
  
• No limitations on export
  
• Slower (calculations repeated many times termed rounds)
  
• You can build a stream cipher from a block cipher
  
• AES is the de facto standard today, replacing DES (Advanced Encryption Standard - Rijndael)
  

Classical ciphers

The pre scientific era. Divided into transposition and substitution ciphers

Transposition
Fixed permutation. Each symbol/character remains the same, but are shuffled/their order has been changed. The permutation is the key itself and is performed on a block basis, hence a block cipher. CLASSICAL → SALCACIS. Character statistics are preserved on output.

Substitution

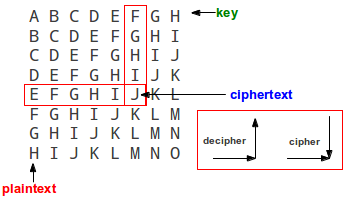
• Mono-alphabetic (A is always B etc). Caesars cipher shifted each character 3 letters later in the (current 23 letter) alphabet. Attacked by letter statistics. Each letter has a different occurrence/probability of appearing in different languages. E usually the most common and Z the less seen. Find the most common letter, deduce the shift (key) and decipher the message. Caesars cipher had a fixed shift. Generally a mono-alphabetic cipher could have a random substitution alphabet and we would then have to use more of the statistics and some language cleverness to break it.
  If there is not a fixed shift for every letter, we got the carnality faculty number of possible keys:
  
  
  
  
  
• Poly-alphabetic (A is first B, then E, then K... before returning to B), Vigenère’s and Beaufort’s ciphers using a code word (key) to represent the variable shift. Used look up tables to simplify workload (no computers at the time). Can be broken by first determining the key length with autocorrelation. Then all letters belonging to each of the keys shifts can be solved as a mono-alphabetic problem. Requires the cipher-text to be lengthy.

  Vigenère
  

  1. plain-text plus key (encipher)
     
  2. key minus cipher-text (decipher)
     
  
  

  Beaufort
  

  1. key minus plain-text (encipher)
     
  2. key minus cipher-text (deciphering)
     
  
  

• One time pad (Vernam cipher): A special case of poly-alphabetic with key length equal to the plaintext. Cannot be broken if key is pure random and the key is never reused. Could also be used binary XOR-ing the plaintext bit stream with a random equally lengthy bitstream. Main problem is distribution of key material. Used for teletypers. One example of hardware is the Teleprinter T 100 (1960) made my Siemens. Binary to text encoding with ITA-2, a 5-bit with a LTRS and FIGS code to separate letters, numbers and special characters. It even has carriage return (CR) and linefeed (LF)
  

The autocorrelation works by comparing the original cipher-text with different versions of a shifted cipher-text by looking for the number of coincidences where the same letter is equal. The number of shifts with the highest value is probably the correct length of the key.

During WW2 these classical ciphers were realized in electromechanical devices to improve speed. One example is the ENIGMA machine having fixed and mobile wheels, each mono-alphabetic. The key consisted of which of the wheels and their ordering, and later in addition the configuration of a permutation board. It had a reflector in order to use the same hardware for both encipherment and decipherment. This lead to a vulnerability one letter could never be replaced with the same letter.

Information Theory

(Slide 40-69)

If your calculator does not have binary logarithm:

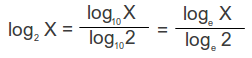
What is perfect security and can we measure how secure a crypto system is? A desirable property of a crypto system is that it should not be breakable even when trying all possible keys. This can be solved using a "one time pad" system. In practical security we settle with computational infeasible (It'll take forever to try all possibilities with today and tomorrows technology)

In perfect security the plain text is statistically independent of the cryptogram. All possible keys will give you all possible plain text and they are equally likely.

A priori information Previously known information to help us determine what decrypted plain texts are unlikely, additional contextual information

Problem is that meaningful plain text represent a very small part of possible plain texts, and the longer the cipher text, the less meaningful plain text you'll have. This is because of the nature of human language/the (Shannon) entropy of the message. The unicity distance (n zero) is a measure of how much cipher text is necessary to obtain only one meaningful decrypted message when brute forcing, and it's a good measure of security. We want it to be infinity.

During all of the formulas X is the plain text, Y the cipher text and Z the key,
L is the cardinality of the coding (binary=2, english language=26..) and n would be the length of the plain, cipher or key.

The entropy and the conditional entropy (equivocation) is defined. Entropy is 1 when we have no confidence and 0 when we have full confidence (deterministic). This is per bit/symbol.

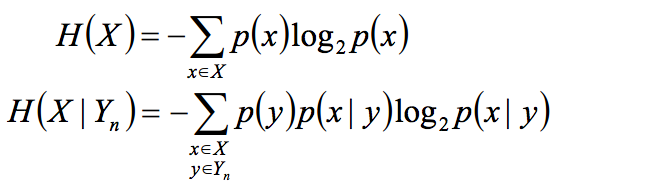
H(X), H(Y) and H(Z) follows the same formula. We want the H(X|Y) "Entropy of plain-text given the cipher-text to be equal to H(X) the "entropy of the plain-text" itself for perfect security.

"The cipher-text should not give us any information about the message"

The rate of the language, the formula for calculating the true rate (r). When the limit of n goes to infinity, the true rate is found. It is found experimentally and is considered a "constant":

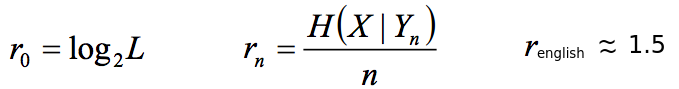
The redundancy of the language: (the rate minus the true rate)

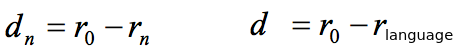
The unicity distance: (the entropy of the key divided by the true redundancy of the language)

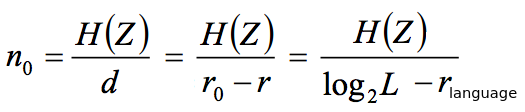
We want unicity distance to be as high as possible, preferable infinity

Increase unicity distance by removing redundancy with source coding

Demonstration of C# code

Look for "vigenere.rar" archive in fronter with examples.
Download a runtime for C# (C Sharp) to run the examples.
Teacher demonstrated how to use the code to solve a poly-alphabetic substitution cipher-text with unknown key length.